Mindestanzahl Profi-Shuffle

Als Misch-Methode kommt die sog. Profi-Shuffle zum Einsatz. Die Frage ist nun, wie oft muss ein Kartenspiel, bestehend aus 52 Karten, gemischt werden, damit jede beliebige Karten-Verteilung möglich ist?

Optimal heißt in diesem Zusammenhang, dass jede mögliche Kartenverteilung nach dem Mischen auftreten kann; als Misch-Methode kommt die sog. Profi-Shuffle zum Einsatz.
Die Frage ist nun, wie oft muss ein Kartenspiel, bestehend aus 52 Karten, gemischt werden, damit jede beliebige Karten-Verteilung möglich ist?

Diese Frage ist nicht so einfach zu beantworten. Es lässt sich jedoch leicht zeigen, dass fünfmaliges Mischen nicht ausreicht.

Satz
n-maliges Mischen eines 52er Kartenspiels ist nicht optimal, n ≤ 5

Vorbereitung
Man denke sich die Karten von 1 bis 52 durchnummeriert.

Definitionen

• Eine K-Sequenz sei eine ununterbrochene Folge 1, 2, 3, ... von Karten – nicht notwendigerweise unmittelbar aufeinander folgend
• Eine K-Sequenz-Anzahl sei dabei die Anzahl aller solcher Folgen.

K-Sequenz-Beispiele

• 1-2-3-...-50-51-52: K-Sequenz-Anzahl = 1
• 1-8-7-3-4-2-5-6: K-Sequenz-Anzahl = 4 (K-Sequenzen: [1-2], [3-4-5-6], [7], [8])
• 52-51-50-...-3-2-1: K-Sequenz-Anzahl = 52

Misch-Beispiel (6 Karten)

• Verteilung vor dem Mischen: 1-2-3-4-5-6
• Splitten: 1-2-3 | 4-5-6
• Verteilung nach dem Mischen (Beispiel): 1-4-5-2-6-3

Beweis

1. Nach dem 1. Mischen gilt: K-Sequenz-Anzahl = 2, wie man sich leicht am obigen Beispiel klarmachen kann.
2. Nach dem 5. Mischen kann die maximale K-Sequenz-Anzahl lediglich 2⁵ = 32 betragen.
3. Eine Kartenverteilung 52-51-...-2-1 besitzt eine K-Sequenz-Anzahl von 52, kann also nicht möglich sein.
4. Mindestens eine Kartenverteilung ist also nach fünfmaligem Mischen nicht erreichbar

qed.

Abschätzung für opimale Anzahl der Mischvorgänge

Vor dem Mischen hat man eine Permutation \(\pi_{vorher}\), nach n-maligem Mischen die Permutation \(\pi_{nachher}\). das Mischen ist also eine Wahrscheinlichkeitsverteilung \(Q\) über die Permutationen: \(Q(\pi_{nachher}\)), wobei für jede Permutation gilt:
\(0 \le Q(\pi_{nachher}) \le 1\), sowie \(\sum_{\pi_{nachher} \in S_{52}} = 1\), \( S_{52} = \{1,\ldots ,52\}\), Anzahl aller Permutationen = \(52!\)

Ein perfektes mischen bedeutet, dass alle Permutationen gleich wahrscheinlich sind, d.h.
\(Q_{perfekt}(\pi_{nachher}) = \frac{1}{52!} \forall \pi_{nachher}\)
Die Funktion \(Q\) ist dabei für die Profi-Shuffle recht kompliziert. Sicherlich ist die Wahrscheinlichkeit abhängig von der Anzahl der Mischvorgänge.

Es wird also ein gutes (mathematisches) Modell mit einer Wahrscheinlichkeitsverteilung \(Q_n\) für nacheinander ausgeführte \(n\) Profi-Shuffles gesucht. Anschließend kann dann die Güte der Mischvorgänge analysiert werden. Ein solches Modell hat die Verteilung:
\(Q_n(\pi_{nachher}) = \Bigg\{ \begin{array} \frac{\binom{2^n+52-r}{52}}\big/{2^{52n}},\; falls\; \pi_{nachher}\; r \le 2^n\;K-Sequenzen\; besitzt\\0,\; falls\; \pi_{nachher}\; r > 2^n\; K-Sequenzen\; besitzt \end{array} \)

Der Abstand zweier Verteilungen kann mit einer sog. “Total Variation Distance (TV)” gemessen werden. Die TV ist wie folgt definiert:
\(\delta(Q_n,Q_{perfekt}):=\frac{1}{2}\sum_{\pi}|Q_n(\pi) - \frac{1}{52!}|\)
Weil die Summe mit /(52!/) Summanden nicht berechenbar ist, führt die Überlegung, dass die meisten Summanden gleich sind, mit:
\(A_{m,r} = \sum_{i=0}^{r-1}(-1)^i\binom{m+1}{i}(r-i)^m \) zu:

\(\delta(Q_n,Q_{perfekt})=\frac{1}{2}\sum_{r=1}^{52}A_{52,r}|\binom{2^n+52-r}{52}\big/2^{52n} - \frac{1}{52!}|\)

Die entsprechende Grafik sieht folgendermaßen aus:

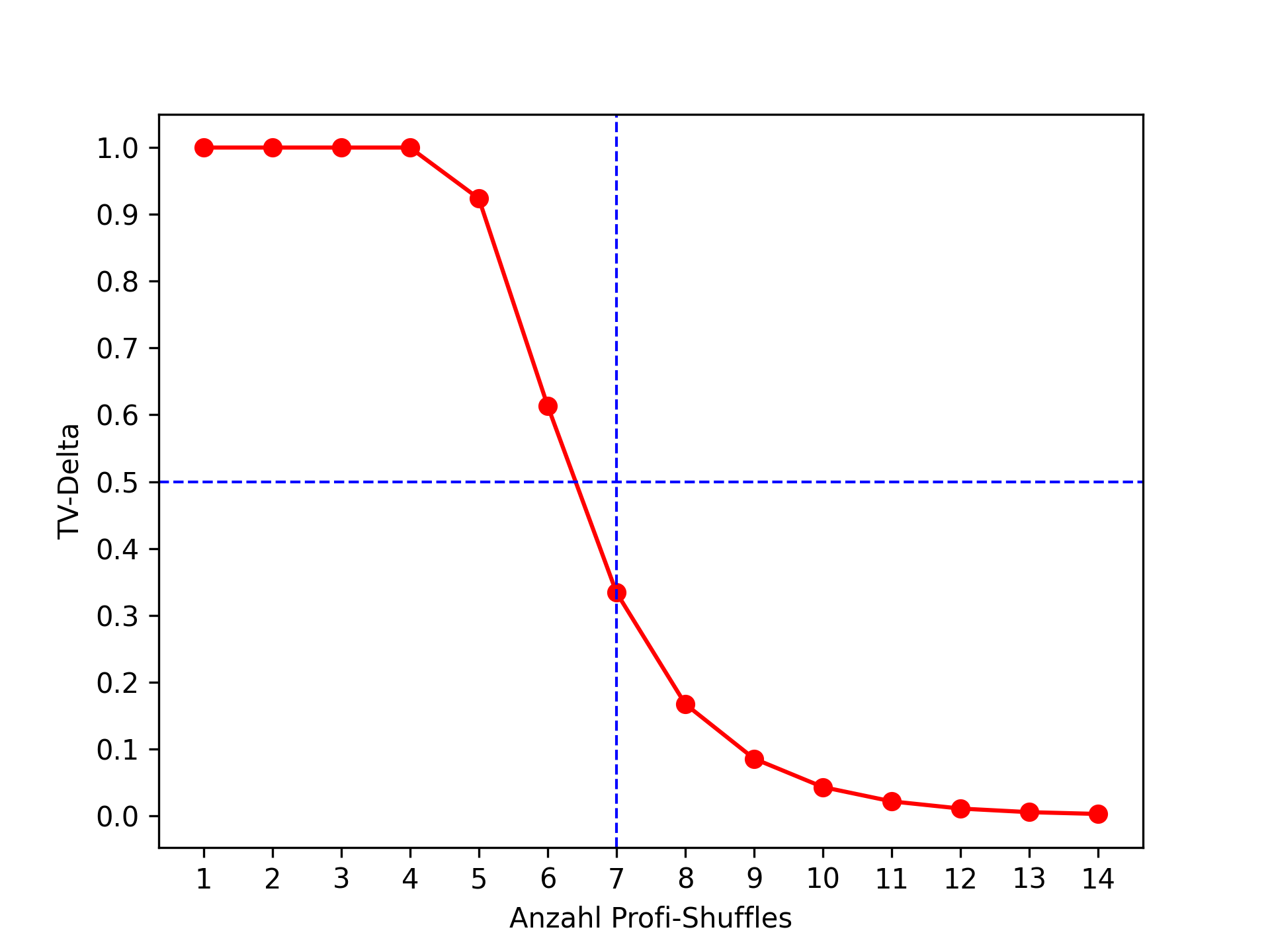
Hieraus folgt, dass 7 eine angemessene Anzahl von Profi-Suffles ist!

Anmerkung: Ausführliche Informationen über alle Aspekt des Mischens von Karten findet man in folgenden Buch:
The Mathematics of Shuffling Cards von Persi Diaconics und Jason Fulman.
So spielt z. B. die Art des Karten-Gebens ebenfalls eine Rolle bzgl. der Anzahl der Mischvorgänge:
Am schlechtesten ist es, jeweils die Anzahl benötigter Karten „am Stück“ reihum zu verteilen.
Am besten ist es, 16 Karten abzuheben und anschließend einzeln 1 Karte, dann rückwärts einzeln, wieder vorwärts einzeln usw.

Letzte Änderung: 2024-04-07